集合とは数の集まりのことです.そして,その集合を構成している数を要素といいます.
例えば次の様なものがあります.
集合:1以上10以下の整数
要素:1,2,3,4,5,6,7,8,9,10
ここからは,この集合を記号を使って書いてみようと思います.
\(A\)という集合があって,その要素として\(a\)という要素があるとします.そのとき
\( \boldsymbol a \in A\)
と書きます.逆に\(b\)という数が要素では無いときは
\( \boldsymbol b \notin A\)
と書きます.
文字だと少し分かりにくいので例を挙げてみましょう.
集合Aを「1以上5以下の整数」とします.すると
1以上5以下の整数は\(1 \in A\),\(3 \in A\)のように書けます.
これ以外の数は\(6 \notin A\),\(-1 \notin A\),\(\displaystyle \frac{1}{2} \notin A\)のようになります.
集合は普通は{}の中に要素を書いて書き表します.例えば次の様な感じです.
\(A=\{1,2,3\}\)
\(B=\{-5,-4,・・・,4,5\}\)
\(C=\{x|x>1,xは実数\}\)
3つ目は1より大きい数の集合という意味です.
集合のうち要素の個数が有限個のものを有限集合,無限のものを無限集合といいます.上の例で言えば集合\(A,B\)は有限集合,集合\(C\)は無限集合です.
続いて部分集合というものについて解説していきます.
部分集合とは例えば\(B\)という集合が\(A\)という集合に含まれていようなとき,\(B\)は\(A\)の部分集合であると言います.このとき\(B \subset A\)と書きます.部分集合の記号は要素の記号(\(\in\))とは違うので注意.
図にすると下の様になります.
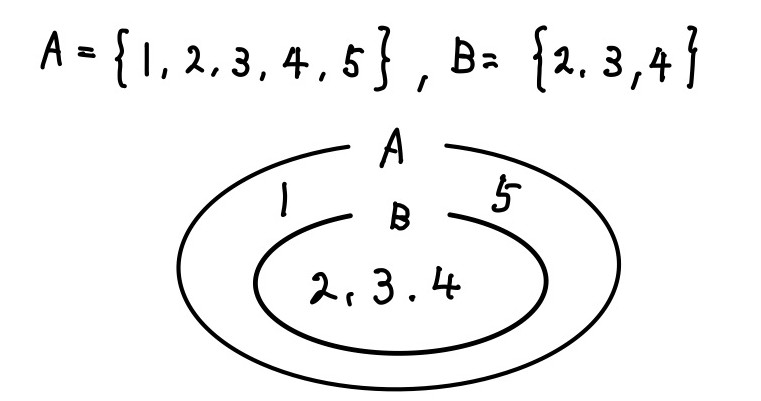
このような円で集合を表した図をベン図といいます.
集合において,当てはまる要素が1つも無い集合を空集合といい\(\emptyset\)という記号で表します.
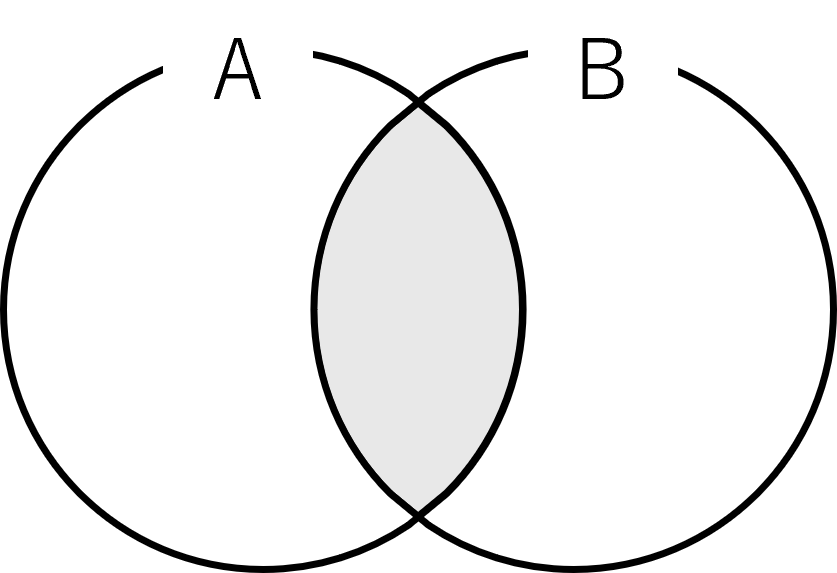
集合には共通部分と和集合というものがあります.
共通部分とはその名の通り2つの集合があったとき共通している数のことです.
集合\(A\)と\(B\)の共通部分は\(A \cap B\)と書き,\(A\)かつ\(B\)と読みます.
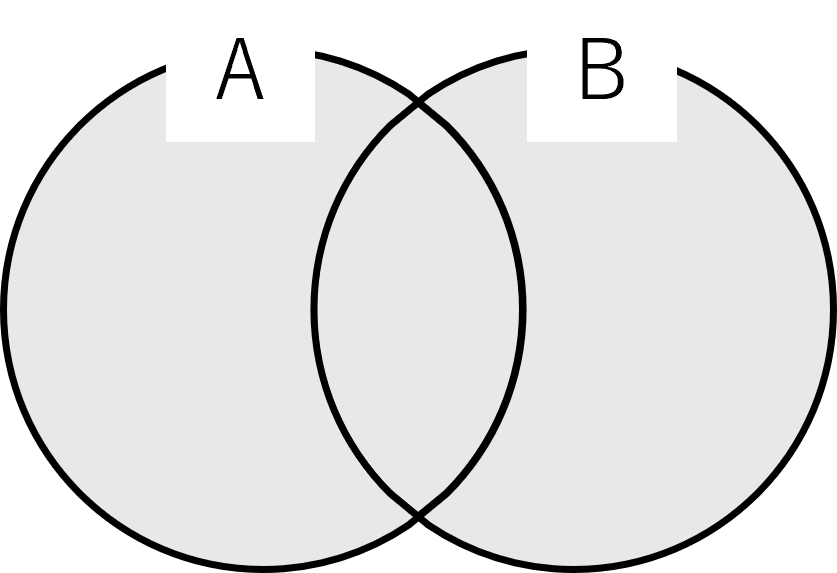
和集合とは2つの集合を合わせた全体の集合のことです.
集合\(A\)と\(B\)の共通部分は\(A \cup B\)と書き,\(A\)または\(B\)と読みます.
図にすると下のようになります.
\(A \cap B\)
\(A \cup B\)
集合\(A\)の要素以外の全ての要素を補集合といい\(\overline{A}\)と書きます.
集合において,初めに「実数全体」など集合の範囲が限定されている場合がほとんどです.このような大枠となる集合を全体集合といい,\(U\)で書きます表します.
補集合の関係についてド・モルガンの法則というものがあります.
\( \overline{A \cup B} = \overline{A} \cap \overline{B}\)
\( \overline{A \cap B} = \overline{A} \cup \overline{B}\)
説明はここまでになります.では早速例題をやってみましょう.
例題
問1.次の集合の要素を全て書け.
(1) \( -1以上3以下 \)の整数全体の集合
(2) \(A=\{ x| 3<x ≦7 ,xは整数\}\)
(3) \(A=\{ 2x-1| 1<x<4 ,xは整数\}\)
問2.集合\(U=\{1,2,3,4,5,6,7,8\}\),\(A=\{1,2,3,4\}\),\(B=\{3,4,5,6\}\)とする.このとき次の集合を答えよ.
(1) \( \overline{A} \)
(2) \( A \cap B \)
(3) \(A \cup B\)
(4) \( \overline{A \cup B}\)
解答
問1.
(1) \(-1,0,1,2,3\)
(2) \(4,5,6,7\)
(3) \(3,5\)
問2.
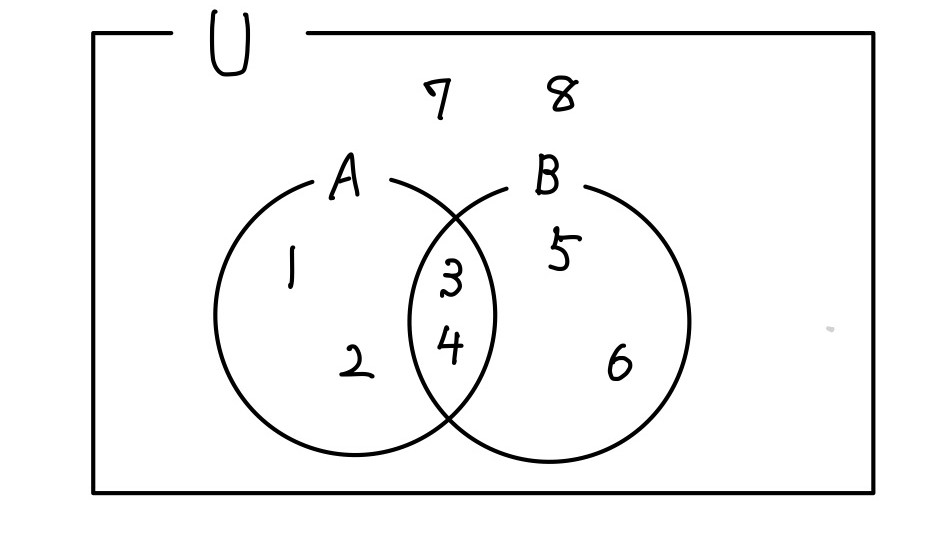
(1) \( \overline{A}=\{3,4,5,6,7,8\} \)
(2) \( A \cap B = \{3,4\}\)
(3) \(A \cup B = \{1,2,3,4,5,6\}\)
(4) \( \overline{A \cup B} = \{7,8\}\)