答えが正しいか正しくないかがはっきりと決まる問を命題といいます.命題が正しいとき,その命題は真,正しくないときは偽であると言います.
命題は「 \(p\) ならば \(q\) 」と書くことが多いです.例えば「 \(x=1\) ならば \(2x=2\) である」のような感じです.
このとき \(p\) 似当たる部分を仮定,\(q\) を結論といいます.
ここで,「 \(p\) ならば \(q\) 」は記号を用いて「 \(p \Rightarrow q\) 」と書きます.
「 \(p \Rightarrow q\) 」という命題を満たさない数をや条件を反例といいます.
例えば,「 \(x^2=1 \Rightarrow x=1\) 」という命題を考えてみましょう.一見正しそうですが,\(x=-1\) も \(x^2=1\) の解です.ですのでこの命題は偽であり,反例は \(x=-1\) ということになります.
\(p\) という条件に対して \(p\) でない条件を \(p\) の否定といい,\(\overline{p}\) と書きます.
「 \(p \Rightarrow q\) 」という命題について,この命題が成り立つとき,\(p\) をこの命題の十分条件,\(q\) を必要条件といいます.また,「 \(p \Rightarrow q\) 」かつ「 \(q \Rightarrow p\) 」のとき,「 \(p \Leftrightarrow q\) 」と書き,これが成り立つとき \(p\) ,\(q\) を必要十分条件といい,\(p\) と \(q\) は同値であると言います.
命題を考える上で非常に重要になってくるのが,逆,裏,対偶です.
- 逆 \(p \Rightarrow q\) の逆は \(q \Rightarrow p\)
- 裏 \(p \Rightarrow q\) の裏は \(\overline{p} \Rightarrow \overline{q}\)
- 対偶 \(p \Rightarrow q\) の対偶は \(\overline{q} \Rightarrow \overline{p}\)
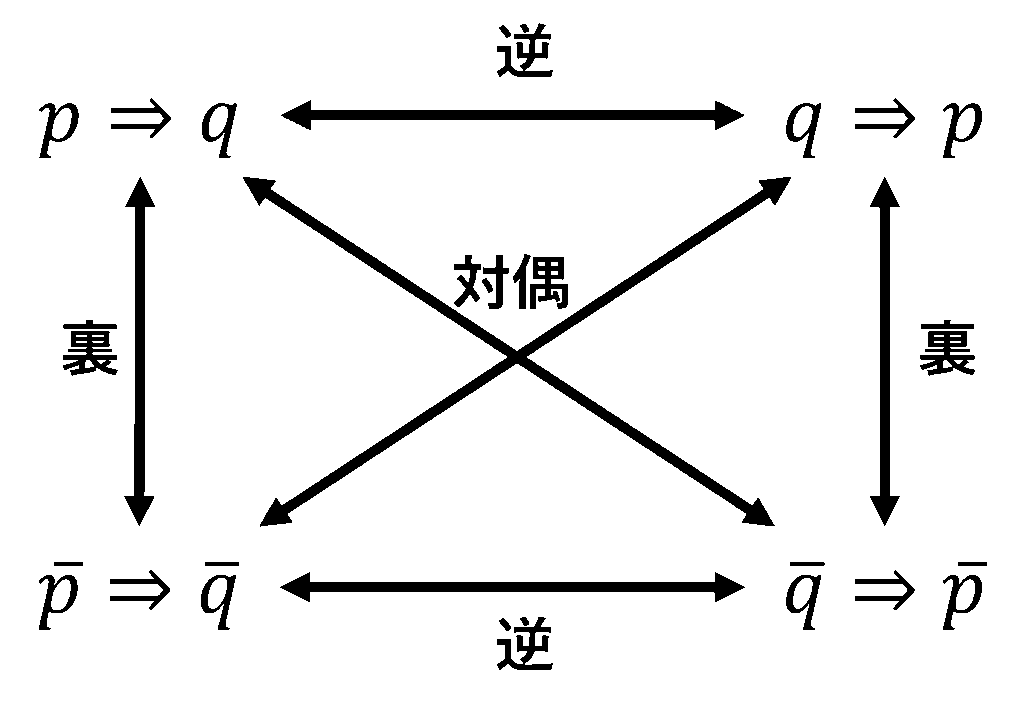
ここで重要なのが「対偶証明法」です.ある命題を証明する際,対偶が真であれば必ずもとの命題も真になります.
ただし,逆や裏は真になるとは限りません.
命題を証明するとき,対偶を利用するということがよくあるのでしっかりと覚えましょう.
最後に背理法です.背理法とは,命題が成り立たないことを仮定して矛盾することを示すことで,もとの命題が真であることを証明する証明法です.
正直,背理法は少し難しいのでここは頑張りましょう.背理法を使った \(\sqrt{2}\) が無理数であることを証明してみます.
問
\(\sqrt{2}\) が無理数であることを証明せよ.
解法
\(\sqrt{2}\) が有理数であると仮定する.
このとき \(\sqrt{2}\) は互いに素である整数 \(a\),\(b\) を用いて,\(\displaystyle \sqrt{2} = \frac{a}{b} \) と書ける.
ここで,両辺を2乗して \(b^2\) をかけると
\(2b^2=a^2\)
となる.
ここで,左辺は2の倍数であるから右辺の \(a^2\) も2の倍数である.ゆえに \(a=2c\) と書ける.
よって \(2b^2=a^2=(2c)^2=4c^2\) より,\(b^2=2c^2\) となる.
右辺が2の倍数であるから左辺も2の倍数になる.ゆえに \(b=2d\) と書ける.
ここで, \(a=2c\) ,\(b=2d\) と表せ,ともに2の倍数になった.しかし,\(a\) ,\(b\) は互いに素であるから,矛盾する.
よって \(\sqrt{2}\) が無理数である.
互いに素・・・1以外の公約数を持たないこと.
背理法は少し難しいですが,「反対のことを証明して矛盾することを示す」と覚えておきましょう.
例題
問1.次の命題の仮定と結論を答えよ.
(1) \(1<x\) ならば \(0<x\) である.
(2) \(2x+1=9\) ならば \(x=4\) である
(3) \(|x|=1\) ならば \(x=1\) である.
問2.問1の各命題について,その逆,裏,対偶及び,その真偽を答えよ.
問3.問1の各命題について,仮定に当たる部分は必要条件,十分条件,必要十分条件,あるいはそのどちらでもないか答えよ
解答
問1.
(1) 仮定 \(1<x\)
結論 \(0<x\)
(2) 仮定 \(2x+1=9\)
結論 \(x=4\)
(3) 仮定 \(|x|=1\)
結論 \(x=1\)
問2.
(1) 逆 \(0<x\) ならば \(1<x\) ,偽 (反例 \(x=0.5\))
裏 \(1≧x\) ならば \(0≧x\) ,偽(反例 \(x=0.5\))
対偶 \(0≧x\) ならば \(1≧x\) ,真
(2) 逆 \(x=4\) ならば \(2x+1=9\) ,真
裏 \(2x+1 \neq 9\) ならば \(x \neq 4\) ,真
対偶 \(x \neq 4\) ならば \(2x+1 \neq 9\) ,真
(3) 逆 \(x=1\) ならば \(|x|=1\) ,真
裏 \(|x| \neq 1\) ならば \(x \neq 1\) ,真
対偶 \(x \neq 1\) ならば \(|x| \neq 1\) ,偽(反例 \(x=-1\))
問3.
(1) 十分条件
(2) 必要十分条件
(3) 必要条件