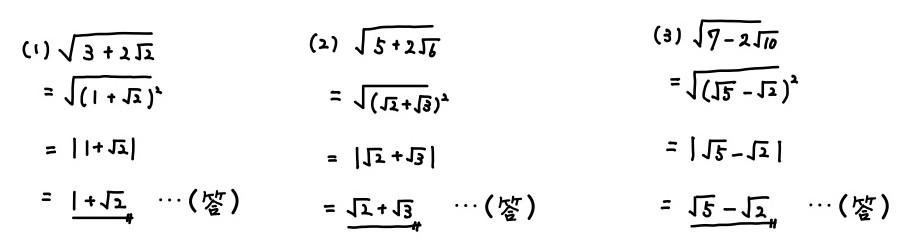有理数と無理数
実数には大きく分けて2つの数があります.それは有理数と無理数です.有理数とは\(\displaystyle \frac{(\text{整数}) }{(\text{整数}) }\) で書ける数のことです.言葉で言われても分からないと思うので例を挙げてみます.
- 有理数・・・\(0.25, 0.333\cdots\) など
- 無理数・・・\(\pi, \sqrt{2}\) など
有理数の例の方では\(\displaystyle \frac{1}{4}\)や\(\displaystyle \frac{1}{3}\)のように\(\displaystyle \frac{(\text{整数}) }{(\text{整数}) }\) で書くことができます.しかし円周率や\(\sqrt{2}\) は循環することなく無限に続く数のため分数で書くことができません.そのため,これらは無理数になります.無限に続く数だからといって,無理数であるとは限らないのでそこは注意してください.
循環小数
次に小数です.小数の中には\(0.123123\cdots\)のようにある一定の周期で同じ数字が繰り返されるものがあります.こういった小数を循環小数と呼びます.そして例えば\(0.1212\cdots\)は繰り返しの初めと終わりの数の上に点を打って\(0. \dot{1} 2 \dot{3}\)のように書きます.
循環小数についてはある決まった問題が出ることがあるので,そのやり方を解説したいと思います.
問
\(0. \dot{1} 2 \dot{3}\)を分数で表せ.
解法
- まず\(x=0.123123\cdots\)とします.
- 次にxを10倍あるいは100倍などして循環している部分の桁がそろうようにします.
今回の場合は1000倍します.すると\(1000x=123.123123\cdots\)となります.小数点以下の123の並びがそろってくれました.
- 続いてこれを引き算してあげます.
下のように筆算すると見やすいです.
そうするときれいに小数点以下がすべて消えてくれました.(このために1000倍しました)
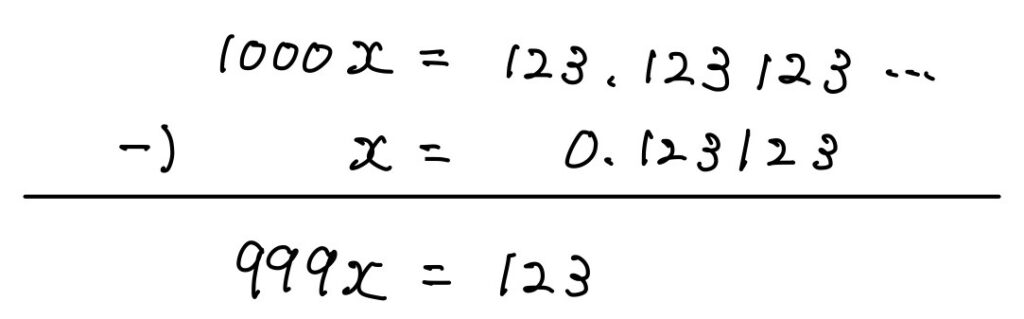
- 最後に式変形して\(x=\)のかたちに直してあげれば終了です.
\begin{align}
999x &= 123 \\
x &= \frac{123}{999} \\
&=\frac{41}{333}
\end{align}
絶対値
続いて絶対値です.中学校で既に習っていると思いますが改めて確認しましょう.絶対値とは数直線上で考えたときの \(0\) からの距離のことです.ですので \(3\) の絶対値は \(3\) ,\(-10\) の絶対値は \(10\) になります.ここで,絶対値を表す新しい記号が出てきますそれが\(\boldsymbol{|a|}\) です.これは \(a\) の絶対値を表します.ですので \(|-5|=5\)ということになります.
平方根
まずは平方根の基本的な公式をおさらいしましょう.
公式
- \(\boldsymbol{(\sqrt{a})^2=|a|}\)
- \(\boldsymbol{\sqrt{a}\sqrt{b}=\sqrt{ab}}\)
- \(\boldsymbol{\displaystyle \frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}}\)
- \(\boldsymbol{\sqrt{t^2a}=t\sqrt{a}}\)
これを利用して,これから新しく重要になってくるのが二重根号に関する事柄です.二重根号とは例えば\(\sqrt{2-\sqrt{3}}\)のようなものです.このように二重で根号が使われてしまっているものの根号を1つ減らしていく方法を解説していきます.ここからは\(\sqrt{2+\sqrt{3}}\)の場合を考えていきます.
解法
- 内側の根号の係数を2にする.
\(\sqrt{2-\sqrt{3}}\)では無理やり分母に2をもってくることで係数を2にします.
\(\displaystyle \sqrt{2-\sqrt{3}}=\sqrt{\frac{4-2\sqrt{3}}{2}}\)
もし\(\sqrt{6+4\sqrt{2}}\)のような場合は
\(\displaystyle \sqrt{6+4\sqrt{2}}=\sqrt{6+2\times 2\sqrt{2}}=\sqrt{6+2\sqrt{2^2\times 2}}=\sqrt{6+2\sqrt{8}}\)
として係数を2にしましょう.
- \(\sqrt{a+\sqrt{b}}\)で足し \(a\) ,かけて\(b\) になる組合わせを考える.
\(\sqrt{2-\sqrt{3}}\)の場合,\(\sqrt{\frac{4-2\sqrt{3}}{2}}\)に注目して,たして4,かけて3になる数を考えます.
すると1と3の組合わせが出てきます.
- 今出てきた1と3を使うと\(2-\sqrt{3}=(\sqrt{3}-\sqrt{1})^2=(\sqrt{3}-1)^2\)と書けます.実際に正しいか展開して確認してみてください.
- これをもとの式に代入して計算していきます.
\begin{align}
\sqrt{2-\sqrt{3}}&=\sqrt{\frac{4-2\sqrt{3}}{2}}\\
&=\sqrt{\frac{(\sqrt{3}-1)^2}{2}}\\
&=\frac{\sqrt{(\sqrt{3}-1)^2}}{\sqrt2}\\
&=\frac{|\sqrt{3}-1|}{\sqrt{2}} \\
&=\frac{\sqrt{3}-1}{\sqrt{2}}
\end{align}
ここで,下から2行目で絶対値にするのを絶対に忘れないでください!
以上で終了です
少し覚えることが多いですが頑張っていきましょう!!
例題
問1.次の数を有理数であるか無理数であるか答えなさい.
(1) \(13\)
(2) \(\sqrt{5}\)
(3) \(\displaystyle \frac{4}{3}\)
(4) \(3.14\)
(5) \(\displaystyle \frac{\sqrt{2}}{3}\)
(6) \(2\pi\)
問2.次の小数を分数で表しなさい.
(1) \(0. \dot1 \)
(2) \(\dot1 . \dot3 \)
(3) \(10.\dot1 \dot2\)
(4) \(1.\dot10\dot2\)
(5) \(0.\dot500\dot1\)
問3.次の式を計算せよ.
(1) \(|3|+|-1|\)
(2) \(|1-3|+2|1+5| \)
(3) \(-|2 \times 3-2| + |3-2 \times 5|\)
問4.次の式を簡単にせよ.
(1) \(\displaystyle \sqrt{3+2\sqrt{2}}\)
(2) \(\displaystyle \sqrt{5+2\sqrt{6}}\)
(3) \(\displaystyle \sqrt{7-2\sqrt{10}}\)
解答
問1.
(1) 有理数
(2) 無理数
(3) 有理数
(4) 有理数
(5) 無理数
(6) 無理数
問2.

問3.
(1)
\begin{align}
&|3|+|-1| \\
=&3+1 \\
=& 4 \cdots \text{(答)}
\end{align}
(2)
\begin{align}
&|1-3|+2|1+5| \\
=&|-2|+2|6| \\
=&2+12 \\
=&14 \cdots \text{(答)}
\end{align}
(3)
\begin{align}
&-|2 \times 3-2| + |3-2 \times 5| \\
=& -|-4|+|-7| \\
=& -4+7 \\
=& 3 \cdots \text{(答)}
\end{align}
問4.