問題
問1.次の不等式を解き,数直線上に範囲を図示せよ.
(1) \(2x+3>-3\)
(2) \(-5x+4≦x-2\)
(3) \(\displaystyle 2x+ \frac{1}{3}≧3x+1\)
(4) \(10x+3>3x+5\)
(5)\(\displaystyle \frac{2}{5}x+\frac{1}{2}≦x-\frac{3}{5}\)
(6) \(\displaystyle -\frac{4}{3}x+\frac{5}{3}>\frac{1}{3}x+\frac{11}{3}\)
問2.次の連立不等式を解きなさい.
(1)
\begin{cases}
2x + 1 > x \\
5x + 2 < 2x+11
\end{cases}
(2)
\begin{cases}
5x-6 ≦ 2x \\
x-1 < 3x+3
\end{cases}
(3)
\begin{cases}
7x+5 ≧ 3x-3 \\
-2x-1 ≦ -x+10
\end{cases}
(4)
\begin{cases}
-x+3≧ -5x+7 \\
7x-5 < 2x+5
\end{cases}
(5)
\begin{cases}
\displaystyle \frac{1}{2}x -3≧ -2x+\frac{5}{2} \\
\displaystyle \frac{1}{3}x+\frac{5}{3} > -x-1
\end{cases}
(6)
\begin{cases}
2x-1 ≧ 5x+2 \\
-x+11 ≧ -7x+5
\end{cases}
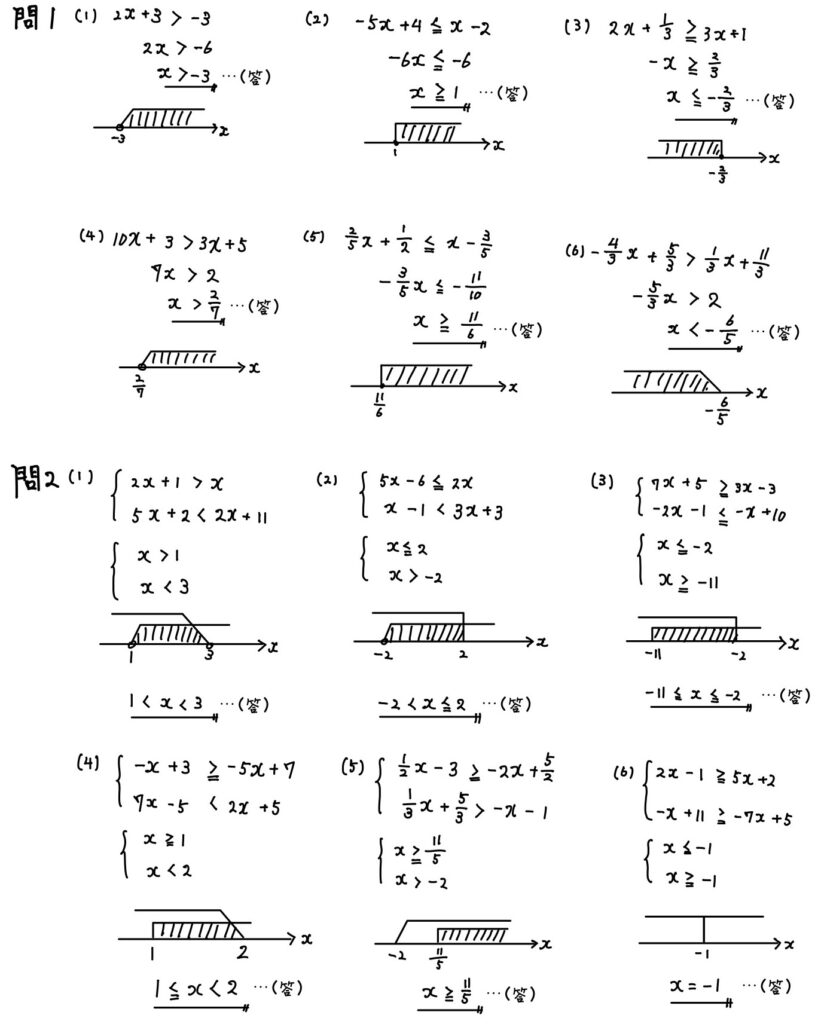
解答