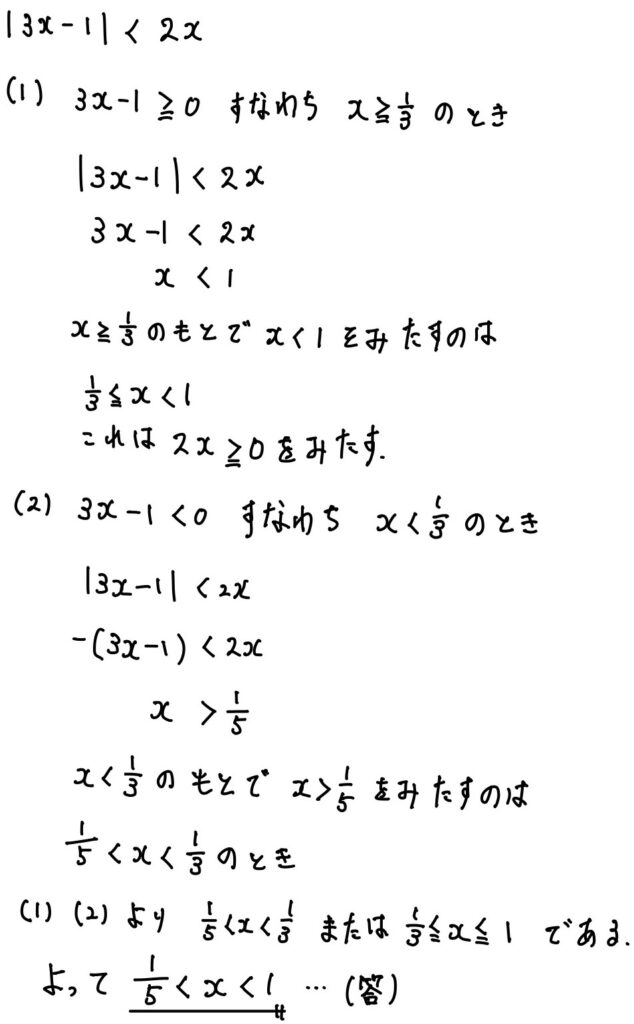不等式とは\(<,>,≦,≧ \)が含まれた式のことです.この単元ではこれらの記号が含まれた式について扱っていきます.
\(<,>,≦,≧ \)の記号の意味を説明しておきます.
- \(a<b\) \(a\)が\(b\)より小さい(\(a=b\)は含まない)
- \(a>b\) \(a\)が\(b\)より大きい(\(a=b\)は含まない)
- \(a≦b\) \(a\)が\(b\)以下である(\(a=b\)は含む)
- \(a≧b\) \(a\)が\(b\)以上である(\(a=b\)は含む)
不等式には以下の関係が成り立ちます.
公式
- \(a<b\)のとき \(\boldsymbol{a+c<b+c}\)
- \(a<b,c>0\)のとき \(\boldsymbol{ac<bc,\displaystyle \frac{a}{c}<\frac{b}{c}}\)
- \(a<b,c<0\)のとき \(\boldsymbol{ac>bc,\displaystyle \frac{a}{c}>\frac{b}{c}}\)
文字で表されると少しわかりにくいと思うので,例題で確認して見てください.
不等式の計算問題に入る前に,数直線の使い方と意味をおさらいしておきます.この単元でとても重要になってくるので,しっかり確認しておきましょう.
数直線上で値の範囲を示すとき下の様な書き方をします.

端の値を含むときはその値の位置から真上に,含まないときは斜めに線を書いてそこから横に伸ばしていきます.また含むときは●,含まないときは○を数直線上に書きます.また,範囲内の部分には斜線を書きます.
続いて,不等式の解き方を解説します.基本的にやり方は方程式と一緒です.
問
(1) \(2x-3<1\),(2) \(-3x+1<7\) を解け
解法
最終的に\(x<\)や\(x≧\)のような形になるように式を変形します.
(1)
まず\(-3\)を右辺に移項します.
すると \(2x<4\)になります.
次に両辺を\(2\)でわって\(x<2\)になります.これで終了です.
(2)
まずは\(1\)を右辺に移項します.
すると\(-3x<6\)になります.
次に両辺を\(-3\)で割ります.このとき注意が必要です.マイナスの数で割るときは不等号の向きが逆になります.
すると\(x>-2\)になります.これで終了です.
上の例のように両辺に正の数をかけたり,割ったりするとき不等号はそのまま,負の数のときは不等号を逆向きにすることを忘れないでください!
このような\(x\)について1次式になる不等式を1次不等式と呼びます.
続いて,連立不等式です.
連立不等式は複数の不等式が組み合わせられたものです.次の例で考えてみましょう.
問
次の連立不等式を解け.
\begin{cases} 2x + 1 > 7 \\ 3x -2 < 19 \end{cases}
解法
- まずは,2つの不等式を解いてあげます.
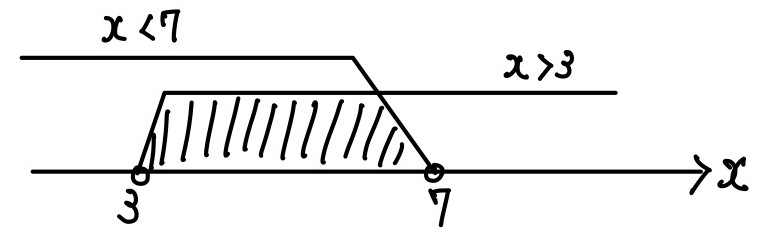
上の不等式は\(x>3\),下の不等式は\(x<7\)と求まります. - 次にこの2つの不等式をドッキングします.
このとき,数直線上で考えてあげると良いでしょう.
数直線上で重なっている部分が今回求める範囲になります.
なので,今回の答えは\(3 < x < 7\)です.
では次に,方程式や不等式に絶対値が含まれる場合を考えます.
絶対値が含まれる場合は次の通り計算します.
- \(\boldsymbol{|x|=a}\) \(\boldsymbol{x=\pm a}\)
- \(\boldsymbol{|x|<a}\) \(\boldsymbol{-a<x<a}\)
- \(\boldsymbol{|x>a|}\) \(\boldsymbol{x<-a,a<x}\)
絶対値が含まれる方程式,不等式の解き方はこの3パターンだけです.これさえできればどんな不等式も解けます.
ここからは少し難しくなります.
\(ax<3\)と\(|x+2|>2x\)という2つの問題を考えましょう.1つ目の問題では\(a\)が正の数か負の数かが分かりません.ですので,それぞれ区別して考えなければなりません.このように異なる場合を考えることを場合分けといいます.2つ目の問題でも同じように場合分けが必要になります.
この2つの問題の解き方を解説していきます.
解法
- \(ax>3\)
(1) \(a>0\)のとき 両辺を\(a\)で割って\(\displaystyle x>\frac{3}{a}\)
(2) \(a=0\)のとき \(0 \cdot x > 3\)となり成り立たない
(3)\(a<3\)のとき 両辺を\(a\)で割って\(\displaystyle x<\frac{3}{a}\)
以上より答えは
\begin{cases}\displaystyle x>\frac{3}{a} \qquad (a > 0 のとき) \\
\displaystyle x<\frac{3}{a} \qquad (a < 0 のとき) \end{cases}
- \(|x+2|<2x\)
\(x+2\)の正負で場合分けをします.ただし,\(|x+2|\)が0以上であることに注意します.
(1)\(x+2≧0\)すなわち\(x≧-2\)のとき
\begin{align}
|x+2|&<2x \\
x+2&<2x \\
x&>2
\end{align}
ここで,\(x≧-2\)という条件であったから,この条件下で\(x>2\)を満たす範囲は\(x>2\)
\(0≦|x+2|≦2x\)より\(0≦2x\)であるはずであるが\(x>2\)はこれを満たす.
(2)\(x+2<0\)すなわち\(x<-2\)のとき
\begin{align}
|x+2|&<2x \\
-(x+2)&<2x \\
x&>-2
\end{align}
ここで,\(x<-2\)という条件であったから,この条件下で\(x>-2\)を満たすことはない.
以上より答えは\(x>2\)
2つ目の問題では絶対値が0以上であることから右辺も0以上になるはずです.その点もちゃんと調べてあげなければなりません.少し細かくて面倒ですが,しっかりチェックするようにしましょう.
ではここまでの内容を例題で確認してみましょう.
例題
問1.次の内容を不等式で表せ.
(1) \(a\)の3倍は\(b\)に\(1\)を加えた値よりも大きい
(2) \(a\)と\(b\)の和は\(c\)以下である
(3) \(a\)の\(2\)倍に\(3\)を加えた値は\(b\)と\(c\)の和の2倍以上である
問2.次の不等式を解いて範囲を数直線上に表しなさい.
(1) \( x+2>5 \)
(2) \( 3x-1≧2 \)
(3) \(2x+9<x+12\)
(4) \( -x+5≦11\)
問3.次の連立方程式を解け.
(1)
\begin{cases}
x + 6 > 7 \\
x -3 < 7
\end{cases}
(2)
\begin{cases}
2x + 2 > x-5 \\
5x -10 < 2x-7
\end{cases}
問4.次の式を解け.
(1) \(|x|=5\)
(2) \(|x+1|=5\)
(3) \(|x|>3\)
(4) \(|x-1|<1\)
問5.\(|3x-1|<2x\)を解け.
解答
問1.
(1) \(3a>b+1\)
(2) \(a+b≦c\)
(3) \(2a+3≧2(b+c)\)
問2.
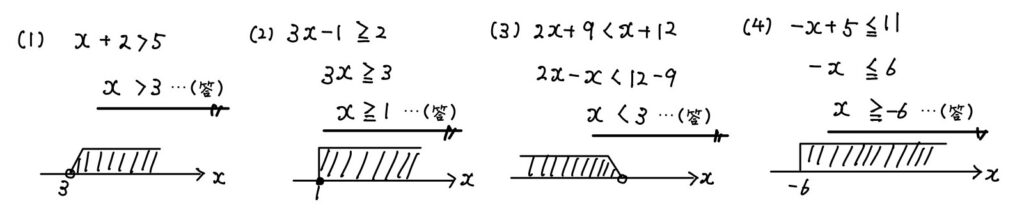
問3.
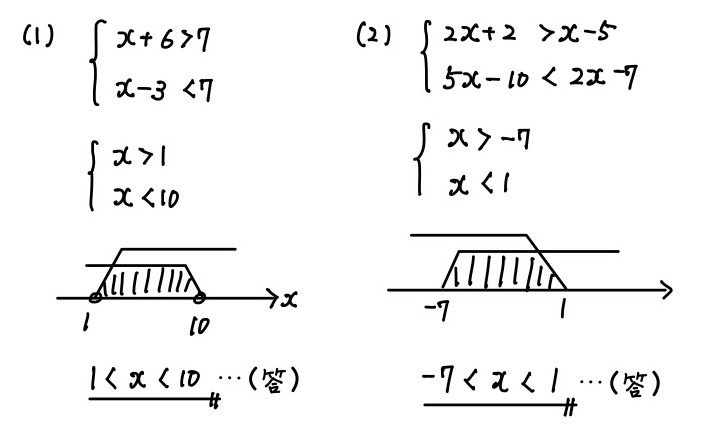
問4.
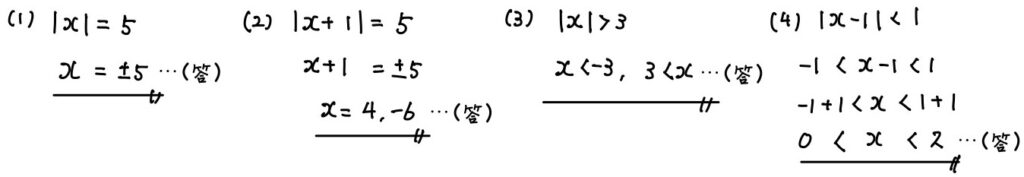
問5.