指数
数学では\(a^n\)という表記がでてきます.この意味は\(a\)を\(n\)回掛けたという意味です.「\(a\)の\(n\)乗」と読みます.また,\(n\)のことを指数といいます.指数の計算には下の3つの公式があります.
公式
- \(\boldsymbol{a^ma^n=a^{m+n}}\)
- \(\boldsymbol{(a^m)^n=a^{mn}}\)
- \(\boldsymbol{(ab)^n=a^nb^n}\)
展開
中学校で既に学んだ展開公式は下の4つです.
公式
- \(\boldsymbol{(x+a)(x+b)=x^2+(a+b)x+ab}\)
- \(\boldsymbol{(a+b)^2=a^2+2ab+b^2}\)
- \(\boldsymbol{(a-b)^2=a^2-2ab+b^2}\)
- \(\boldsymbol{(a+b)(a-b)=a^2-b^2}\)
展開の基本はこれらの式ですがプラスで下の5つの公式も覚えましょう.これらの公式は今後非常に重要になってきます.
公式
- \(\boldsymbol{(a+b)^3=a^3+3a^2b+3ab^2+b^3}\)
- \(\boldsymbol{(a-b)^3=a^3-3a^2b+3ab^2-b^3}\)
- \(\boldsymbol{(a+b)(a^2-ab+b^2)=a^3+b^3}\)
- \(\boldsymbol{(a-b)(a^2+ab+b^2)=a^3-b^3}\)
- \(\boldsymbol{(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca}\)
ただ覚えるのは大変なので,いろいろ問題を解いて覚えていきましょう.
因数分解
展開がきたということはもちろん因数分解もあります.こっちは,展開の真逆をやるだけなので,展開が分かってしまえば簡単です.公式は以下の通りです.
公式
- \(x^2+(a+b)x+ab=(x+a)(x+b)\)
- \(a^2+2ab+b^2=(a+b)^2\)
- \(a^2-2ab+b^2=(a-b)^2\)
- \(a^2-b^2=(a+b)(a-b)\)
- \(\boldsymbol{a^3+3a^2b+3ab^2+b^3=(a+b)^3}\)
- \(\boldsymbol{a^3-3a^2b+3ab^2-b^3=(a-b)^3}\)
- \(\boldsymbol{a^3+b^3=(a+b)(a^2-ab+b^2)}\)
- \(\boldsymbol{a^3-b^3=(a-b)(a^2+ab+b^2)}\)
- \(\boldsymbol{a^2+b^2+c^2+2ab+2bc+2ca=(a+b+c)^2}\)
因数分解について,もう一つ超重要な解き方があります.それがたすき掛けです.例えば,\(6x^2+11x+4\)の因数分解を考えてみましょう.たすき掛けのやり方は以下の通りです.
- まず,\(x^2\)の係数と定数項の部分に注目します.今回はかけて 6 と 4 になる組合わせを考えます.この組合わせはそれぞれ\((1,6)\),\((2,3)\)と\((1,4)\),\((2,2)\)です.
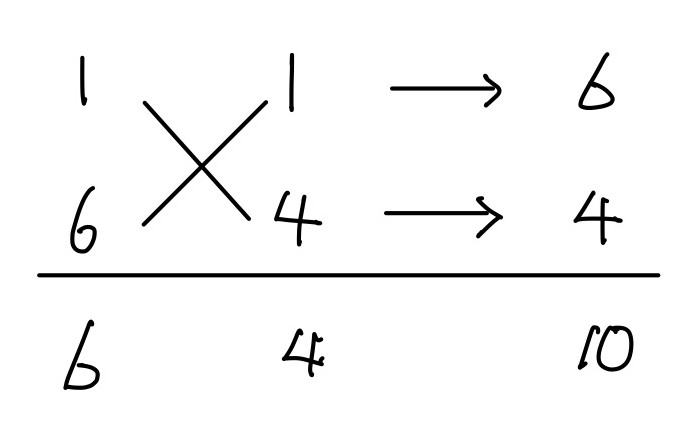
- 次に下のように図を書きます.まず1番左の列にかけて 6 になる組合わせ,2番目に列にかけて 4 になる組合わせを書きます.次に数字同士を線をクロスさせて結んであげます.そして,右側には結ばれた数字同士を掛けた数を書きます.最後に,一番下の段に左2つは上に数を掛けた値を,一番右には足した数を書きます.最終的に一番下の数が左から順に\(x^2\)の係数,定数項,\(x\)の係数になっていればOKです.
下では 6, 4, 10 になってしまいました.6, 4, 11 の組合わせを見つけたいので上で挙げた\((1,6)\),\((2,3)\)と\((1,4)\),\((2,2)\)の組合わせを変えていろいろ調べていきます.
- 調べていくと下の組合わせが見つかります.見つかったら後は簡単です.クロスされた数字の部分だけ注目して横に読んでいきます.すると\((2, 1)\)と\((3, 4)\)になっています.この数字を使って\((2x+1)(3x+4)\)と順番通り書いてあげれば終了です.
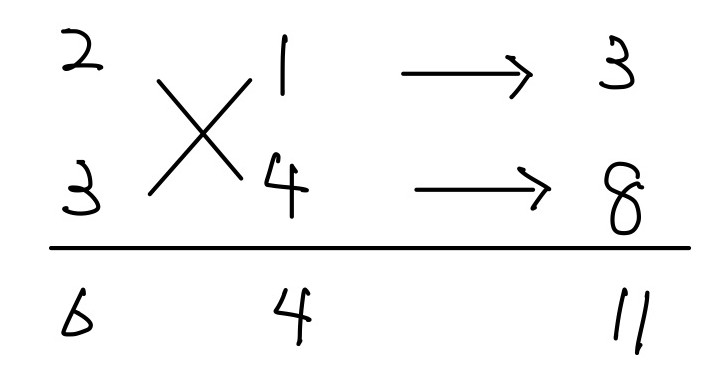
それでは説明はここまでになります.ここからは問題を解いてなれていきましょう.
例題
問1.次の式を展開しなさい.
(1) \((3x+1)(2x-4)\)
(2) \((2x-9)^2\)
(3) \((5x+3)(5x-3)\)
(4) \((9x+1)^2\)
(5) \((x+1)^3\)
(6) \((x-3)^3\)
(7) \((x-2)(x^2+2x+4)\)
(8) \((x+1)(x^2-x+1)\)
(9) \((x+2y+3z)^2\)
問2.次の式を因数分解しなさい.
(1) \(x^2+10x+25\)
(2) \(4x^2-9y^2\)
(3) \(\displaystyle x^2-x+\frac{1}{4}\)
(4) \(x^3+6x^2+12x+8\)
(5) \(x^3+8y^3\)
(6) \(x^3-9x^2+27x-27\)
(7) \((27x^3-y^3)\)
(8) \(3x^2+8x+5\)
(9) \(5x^2-4x-1\)
解答
問1.
(1)
\begin{align}
&(3x+1)(2x-4)\\
=&6x^2-12x+2x-4\\
=&6x^2-10x-4 \cdots \text{(答)}
\end{align}
(2)
\begin{align}
&(2x-9)^2\\
=&4x^2-2 \cdot 2x \cdot 9 +81\\
=&4x^2-36x+81 \cdots \text{(答)}
\end{align}
(3)
\begin{align}
&(5x+3)(5x-3)\\
=&25x^2-9 \cdots \text{(答)}
\end{align}
(4)
\begin{align}
&(9x+1)^2\\
=&81x^2+18x+1 \cdots \text{(答)}
\end{align}
(5)
\begin{align}
&(x+1)^3\\
=&x^3+3x^2+3x+1 \cdots \text{(答)}
\end{align}
(6)
\begin{align}
&(x-3)^3\\
=&x^3-3 \cdot x^2 \cdot 3 +3 \cdot x \cdot 3^2 -3^3 \\
=&x^3-9x^2+27x-27 \cdots \text{(答)}
\end{align}
(7)
\begin{align}
&(x-2)(x^2+2x+4)\\
=&x^3-2^3\\
=&x^3-8 \cdots \text{(答)}
\end{align}
(8)
\begin{align}
&(x+1)(x^2-x+1)\\
=&x^3+1 \cdots \text{(答)}
\end{align}
(9)
\begin{align}
&(x+2y+3z)^2\\
=&x^2+(2y)^2+(3z)^2+2 \cdot x \cdot 2y + 2 \cdot 2y \cdot 3z + 2 \cdot 3z \cdot x\\
=&x^2+4y^2+9z^2+4xy+12yz+6zx \cdots \text{(答)}
\end{align}
問2.次の式を因数分解しなさい.
(1)
\begin{align}
&x^2+10x+25\\
=&(x+5)^2 \cdots \text{(答)}
\end{align}
(2)
\begin{align}
&4x^2-9y^2\\
=&(2x+3y)(2x-3y)\cdots \text{(答)}
\end{align}
(3)
\begin{align}
&x^2-x+\frac{1}{4}\\
=&\Big(x-\frac{1}{2}\Big)^2\cdots \text{(答)}
\end{align}
(4)
\begin{align}
&x^3+6x^2+12x+8\\
=&x^3+3 \cdot 2 \cdot x^2 + 3 \cdot 2^2 \cdot x +2^3\\
=&(x+2)^3 \cdots \text{(答)}
\end{align}
(5)
\begin{align}
&x^3+8y^3\\
=&x^3+(2y)^3\\
=&(x+2y)(x^2-2xy+4y^2) \cdots \text{(答)}
\end{align}
(6)
\begin{align}
&x^3-9x^2+27x-27\\
=&x^3-3 \cdot 3 \cdot x^2 + 3 \cdot 3^2 \cdot x -3^3\\
=&(x-3)^3 \cdots \text{(答)}
\end{align}
(7)
\begin{align}
&27x^3-y^3\\
=&(3x)^3-y^3\\
=&(3x-y)(9x^2+3xy+y^2) \cdots \text{(答)}
\end{align}
(8)
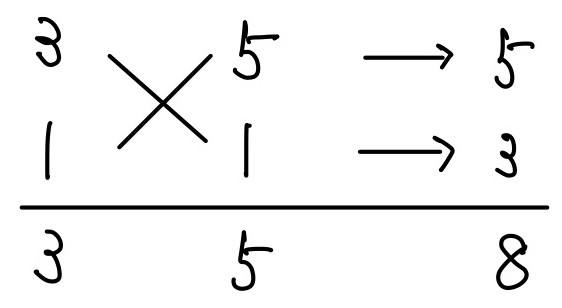
\begin{align}
&3x^2+8x+5\\
=&(3x+1)(5x+1) \cdots \text{(答)}
\end{align}
(9)
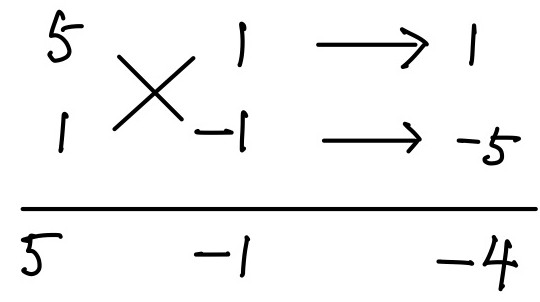
\begin{align}
&5x^2-4x-1\\
=&(5x+1)(x-1) \cdots \text{(答)}
\end{align}