場合の数とはある事柄が何通りあるかということです.例えば赤,青,黄色の三色のボールから1つ選ぶときの場合の数は3通りです.このように,何通りあるか調べることと覚えておきましょう.
場合の数を考える上で,数学Ⅰでも出てくる「集合」の考え方が重要になってきます.集合についてはこちらで確認してください.
ある集合\(A\)に対して,その要素の数を\(n(A)\)で表します.
例えば,\(A=\{1, 2, 3\}\)とすると,\(n(A)=3\)になります.
場合の数を考えるときに重要になるのは次の式のような考えからです.
\(n(A \cup B) = n(A) + n(B) – n(A \cap B)\)
いつこの考え方を使うのか例題で考えてみましょう.
問
1以上50以下の整数において,2の倍数または3の倍数であるものはいくつあるか答えよ.
解法
今回は集合\(U, A, B\)をそれぞれ全集合,2の倍数の集合,3の倍数の集合とおきましょう.
このとき,\(n(A)=25\),\(n(B)=16\)になります.
次に\(n(A \cap B)\)を考えてみましょう.今回,\(A \cap B\) とはすなわち2の倍数かつ3の倍数なので,6の倍数ということになります.ですので6の倍数の個数\(n(A \cap B)=8\)となります.このとき,個数は普通に数えましょう.
そうすると,さっきの式を用いると
\begin{align}
n(A \cup B) & = n(A) + n(B) – n(A \cap B) \\
& = 25 + 16 -8 \\
& = 33
\end{align}
よって,2の倍数または3の倍数は33個となります.
この解き方を図を使って確認してみましょう.図がある方がイメージしやすいと思います.
今回の状況は図にすると下の様になります.
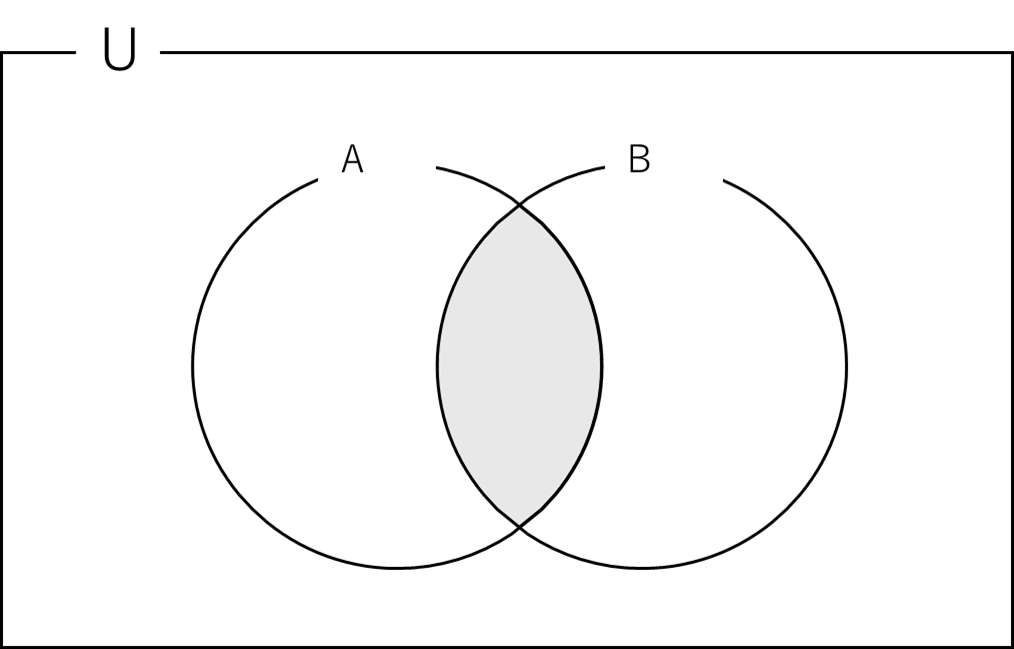
\(A\)が2の倍数,\(B\)が3の倍数,重なっている部分が\(A \cap B\)で6の倍数です.
\(n(A \cup B) = n(A) + n(B) – n(A \cap B)\)の式について図を見ながら考えてみましょう.
\( n(A) + n(B) \)だけでは\(A \cap B\)の部分がダブってしまいます.そこで\(n(A \cap B)\)をⅠ回引いてあげています.そうするとダブり無く\(n(A \cup B)\)になってくれます.
どうでしょう,図を見て何をやっているかイメージできましたか?
【発展】
余裕があればここも考えてみてください.
今度は,3つの集合の場合を考えてみます.まず式としては次の様な関係が成り立ちます.
\(n(A \cup B \cup C) = n(A) + n(B) + n(C) – n(A \cup B) – n(B \cup C) – n(C \cup A) + n(A \cap B \cap C)\)
これもまた図で考えてみましょう.
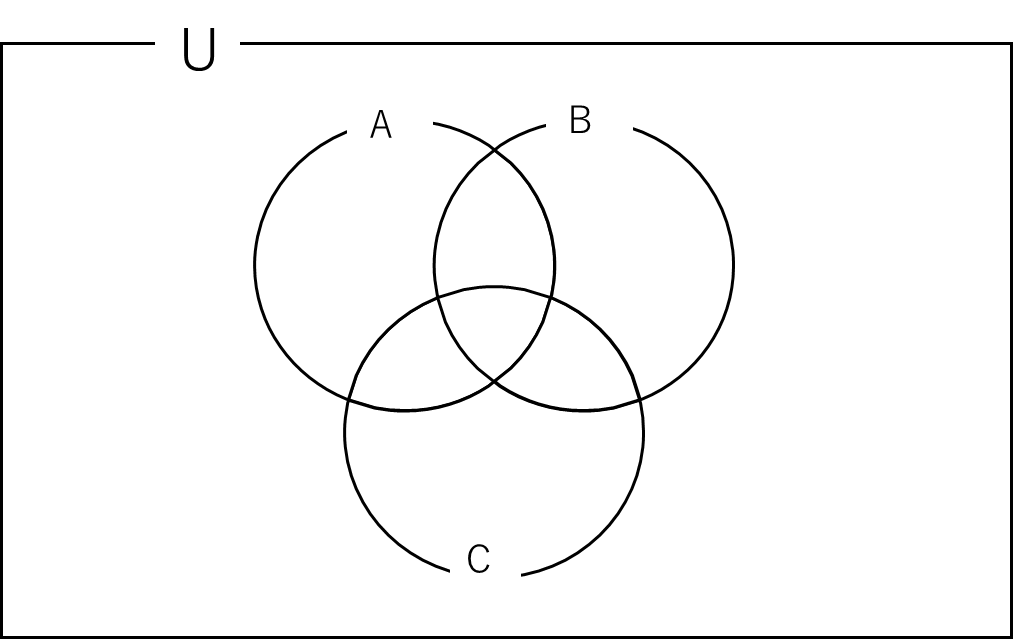
\(A\)または\(B\)または\(C\)を考えます.
まずは\(n(A) + n(B) + n(C)\)で\(A, B, C\)の全てを足し算します.
すると下の3箇所がダブってしまいます.そこで,これらを1回ずつ引いてあげるために\( – n(A \cup B) – n(B \cup C) + n(C \cup A) \)を計算します.
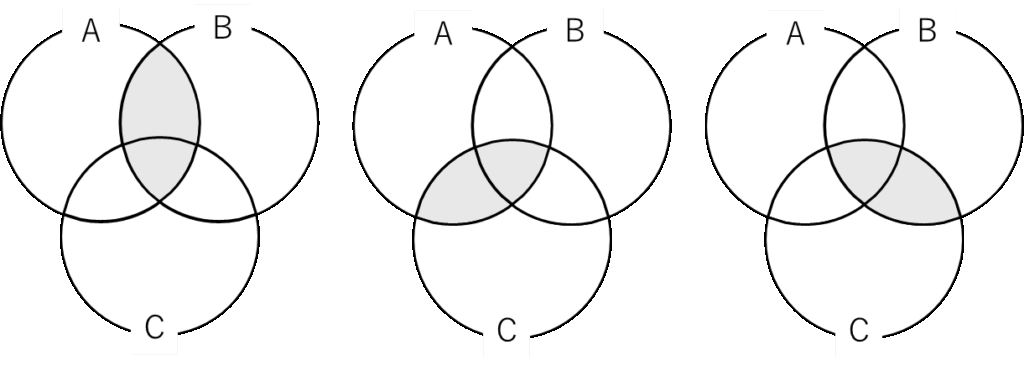
しかし,今度は下の真ん中の部分が足りなくなってしまいます.ですので最後にこの部分を加えるために\( n(C \cup A) \)を足してあげます.
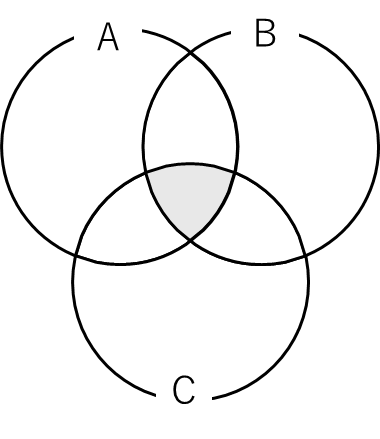
以上のようにすることで
\(n(A \cup B \cup C) = n(A) + n(B) + n(C) – n(A \cup B) – n(B \cup C) – n(C \cup A) + n(A \cap B \cap C)\)
となります.
少し難しいかもしれませんが,パズルだと思って考えてみてください.
場合の数を考える上で,順列と組合わせという2つが出てきます.まずはこの違いをしっかりと理解しましょう.
順列とは\(n\)個ある中から\(k\)個選んで順番に並べるとき何通りあるかということです.「並べる」というのがポイントです.
一方で,組合わせとは\(n\)個ある中から\(k\)個選んだとき何通りあるかということです.
例を挙げて考えてみましょう.赤,青,黄のボールから3球選ぶ場合を考えます.
まずは順列です.順列の場合選んでから並べるので{赤,青,黄},{赤,黄,青},{青,赤,黄},{青,黄,赤},{黄,青,赤},{黄,赤,青}の6通りになります.
続いて組合わせです.組合わせはただ選ぶだけなので,順番は関係ありません.ですのでこの場合組合わせは1通りになります.
順列
ここからは順列について詳しく見ていきます.
順列を考えるときには,次の公式を使います.
\(n\)個の中から\(r\)個を並べる際の順列の総数
\(_nP_r = n(n-1) \cdots (n-r+1)\)
文字だと少し分かりにくいと思うので\(_6P_3\)を考えてみましょう.この場合
\(_6P_3=6 \cdot 5 \cdot 4 = 120\)となります.
このように\(P\)の左下の数字から初めて1つずつ小さくしていき,それを右下に書いてある数だけ続けます.今回の場合は\(6\)からはじめて\(4\)まで3つかけ算します.
数学では\(5!\)のように\(!\)という記号が出てきます.これは階乗と呼び,\(5!=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120\)のようにその数から\(1\),まで全てかけていきます.
これを使うと\(_nP_r\)は次の様に書くこともできます.
\(\displaystyle _nP_r=\frac{n!}{(n-r)!}\)
また,4人全員を並べる様なときは階乗を使って\(4! = 24\)通りのように計算します.
円順列
\(1, 2, 3, 4, 5\)を円形に並べるときの場合の数を考えてみます.
このときの解き方は次の通りです.
- 1つ固定する
- 残りの順列を考える
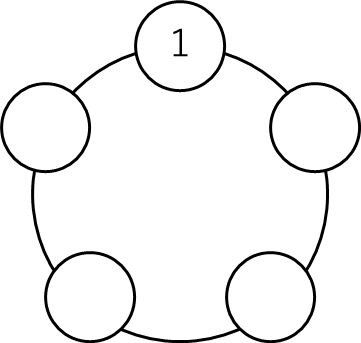
まずは,なんでも良いので1つ固定しましょう.今回は\(1\)を固定するとしましょう.
そうしたら残りは\(2~5\)の4つです.なので\(4! = 24\)となります.
よって,24通りとなります.
重複順列
重複して選ぶことができる場合は\(P\)は使えません.
\(1, 2, 3, 4, 5\)を重複して並べるときは\(5^5=3125\)通りとなります.
なぜこのようになるのか考えてみましょう.
まずは重複が無い場合です.5つの枠に数字を当てはめていくと考えてみましょう.すると,1つ目の枠に入るのは5通りです.続いて2つ目の枠に入るのは,すでに1つ選んでいるので4通りになります.同様に3枠目は3通り,4枠目は2通り,5枠目は1通りです.よって\(5!\)となります.
一方で重複がある場合は1枠目から5枠目までいずれも5通りの選び方ができるため\(5^5\)となります.
組合わせ
次に組合わせです.組合わせでは\(P\)の代わりに\(C\)を使います.\(C\)とは次の式で定義されます.
\(n\)個の中から\(r\)個を選ぶ際の総数
\(\displaystyle _nC_r = \frac{_nP_r}{r!} = \frac{n(n-1)\cdots (n-r+1)}{r(r-1)\cdot1} \)
\(\displaystyle _nC_r=\frac{n!}{(n-r)!r!}\)
ただし,\(_nC_n=1, _nC_0=1\)
また,次の関係が成り立ちます.
\(_nC_r = _nC_{n-r}\) (\(0≦r≦nのとき\))
\(_nC_r = _{n-1}C_{r-1}+_{n-1}C_r\) (\(1≦r≦n-1,n≧2のとき\))
組合わせは\(\displaystyle _nC_r = \frac{_nP_r}{r!} \)の形が最も分かりやすいと思います.順列を\(r!\)で割ります.
また,\(_nC_r = _nC_{n-r}\)の関係は非常に重要です.
例えば\(_8C_7\)を考えてみましょう.
このとき,\(\displaystyle _8C_7 = \frac{8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2}{7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}\)と計算するのは面倒です.そこで,この関係を使いましょう.これを使うと\(_8C_7 = _8C_1\)となります.よって\(_8C_1=8\)と求まります.
ここで,\(\displaystyle _nC_1=\frac{n}{1}=n\)なので\(_nC_1=n\)となります.これは覚えてしまいましょう.
\(_nC_r = _nC_{n-r}\),\(_nC_r = _{n-1}C_{r-1}+_{n-1}C_r\)の証明はこちらで解説します.
順列と組合わせは問題のパターンがほとんど決まっているので,次のページで例題を解きながらやっていきましょう.